Solution of System of Linear Homogeneous and Nonhomogeneous Equations
Applications of Matrices: Consistency of System of Linear Equations by Rank Method
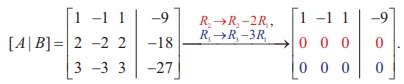
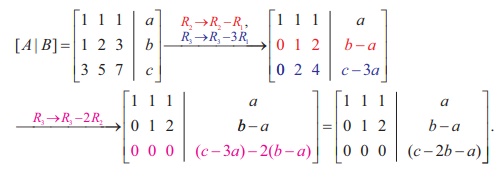
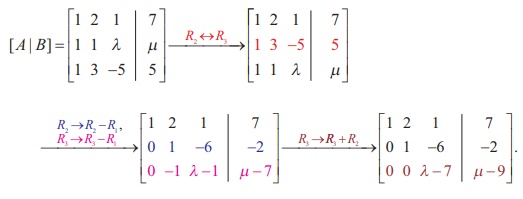
In second previous section, we have already defined consistency of a system of linear equation. In this section, we investigate it by using rank method. We state the following theorem without proof: A system of linear equations, written in the matrix form asAX = B, is consistent if and only if the rank of the coefficient matrix is equal to the rank of the augmented matrix; that is, ρ (A) = ρ ([A|B]). We apply the theorem in the following examples. Non-homogeneous Linear Equations Example 1.29 Test for consistency of the following system of linear equations and if possible solve: x + 2y−z= 3, 3x−y+ 2z= 1,x− 2y+ 3z= 3,x−y+z+1 = 0 . Solution Here the number of unknowns is 3. The matrix form of the system is AX = B, where Applying Gaussian elimination method on [ A | B], we get There are three non-zero rows in the row-echelon form of [A | B].So, ρ ([A | B] ) . = 3 So, the row-echelon form of A is Hence, ρ(A) = ρ([ A | B ]) = 3. From the echelon form, we write the equivalent system of equations x + 2y –z =3, 7y-5z = 8, z=4, 0=0. The last equation 0 = 0 is meaningful. By the method of back substitution, we get z = 4 7y - 20 = 8 ⇒ y = 4 , x = 3 - 8 + 4 ⇒ x = −1. So, the solution is (x = −1, y = 4, z = 4) .(Note that A is not a square matrix.) Here the given system is consistent and the solution is unique. Example 1.30 Test for consistency of the following system of linear equations and if possible solve: 4x− 2y+ 6z= 8,x+y− 3z= −1, 15x− 3y+ 9z= 21. Solution Here the number of unknowns is 3. The matrix form of the system isAX=B, where Applying elementary row operations on the augmented matrix[A|B], we get So,ρ(A) =ρ([A|B]) = 2 < 3. From the echelon form, we get the equivalent equations x +y- 3z= -1,y- 3z= -2 , 0 = 0 . Theequivalentsystemhastwonon-trivialequationsandthreeunknowns.So,oneoftheunknowns should be fixed at our choice in order to get two equations for the other two unknowns.Wefixzarbitrarily as a real numbert, and we gety=3t - 2,x=-1- (3t - 2) +3t =1.So, the solutionis ( x = 1,y = 3t -2, z = t ), where t isreal.Theabovesolutionsetisaone-parameterfamilyofsolutions. Here,thegivensystemisconsistentandhasinfinitelymanysolutionswhichformaoneparameter family of solutions. Note Intheaboveexample,thesquarematrix A issingularandsomatrixinversionmethodcannotbe appliedtosolvethesystemofequations.However,Gaussianeliminationmethodisapplicableandwe are able to decide whether the system is consistent or not. The next example also confirms the supremacy of Gaussian elimination method over othermethods. Example 1.31 Test for consistency of the following system of linear equations and if possible solve: x −y+z= −9, 2x− 2y+ 2z= −18, 3x− 3y+ 3z+ 27 = 0. Solution Here the number of unknowns is 3. The matrix form of the system isAX=B, where Applying elementary row operations on the augmented matrix[A|B], we get So,ρ(A) =ρ([A|B]) = 1 < 3. Fromtheechelonform,wegettheequivalentequations x - y + z =-9, 0 = 0,0 = 0. Theequivalentsystemhasonenon-trivialequationandthreeunknowns. Taking y = s, z = t arbitrarily,weget x - s + t = -9; or x =-9+ s - t. So, the solution is ( x = -9 +s- t , y=s,z=t ), wheresandtare parameters. The above solution set is a two-parameter family of solutions. Here, the given system of equations is consistent and has infinitely many solutions which form a two parameter family of solutions. Example 1.32 Test the consistency of the following system of linear equations x −y+z= −9, 2x−y+z= 4, 3x−y+z= 6, 4x−y+ 2z= 7. Solution Here the number of unknowns is 3. The matrix form of the system of equations isAX=B, where Applying elementary row operations on the augmented matrix [A|B], we get So, ρ (A) = 3 and ρ ([ A | B]) = 4. Hence ρ ( A) ≠ ρ ([ A | B]). If we write the equivalent system of equations using the echelon form, we get x - y + z = -9, y-z= 22, z=-23,0 = -11. The last equation is a contradiction. Sothegivensystemofequationsisinconsistentandhasnosolution. ByRouché-Capellitheorem,wehavethefollowingrule: · Ifthereare n unknownsinthesystemofequationsand ρ ( A ) = ρ ([ A | B]) = n, then the system AX =B, is consistent and has a unique solution. · If there are n unknowns in the system AX =B, and ρ ( A )=ρ([A|B]) =n- k , k≠ 0 then the system is consistent and has infinitely many solutions and these solutions form a k - parameter family. Inparticular,ifthereare 3 unknownsinasystemofequationsand ρ ( A ) = ρ ([ A | B]) = 2, then the system has infinitely many solutions and these solutions form a one parameterfamily.In the same manner, if there are 3 unknowns in a system of equationsand ρ ( A ) = ρ ([ A | B]) = 1, thenthesystemhasinfinitelymanysolutionsandthese solutions form a two parameter family. · If ρ ( A ) ≠ρ ([A|B]), then the system AX =B is inconsistent and has nosolution. Find the condition on a, b and c so that the following system of linear equations has one parameter family of solutions: x + y + z = a, x + 2 y + 3z = b, 3x + 5 y + 7z = c. Solution Here the number of unknowns is 3. The matrix form of the system isAX=B, whereA= Applying elementary row operations on the augmented matrix [A|B], we get In order that the system should have one parameter family of solutions, we must haveρ(A) =ρ([A,B]) = 2. So, the third row in the echelon form should be a zero row. So,c- 2b-a= 0 ⇒ c=a+ 2b. Investigate for what values ofλandμthe system of linear equations x + 2y+z= 7,x+y+λ z=μ,x+ 3y− 5z= 5 has (i) no solution (ii) a unique solution (iii) an infinite number of solutions. Herethenumberofunknownsis 3. The matrix form of the system isAX=B, whereA= Applying elementary row operations on the augmented matrix [A|B], we get (i) If λ = 7 and μ ≠ 9 , then ρ (A) = 2 and ρ ([ A | B]) = 3. So ρ ( A) ≠ ρ ([ A | B]). Hence the given system is inconsistent and has no solution. (ii) If λ ≠ 7 and m is any real number, then ρ (A) = 3 and ρ ([ A | B]) = 3. So ρ (A) = ρ ([ A | B]) = 3 = Number of unknowns. Hence the given system is consistent and has a unique solution. (iii) If λ = 7 and μ = 9, then ρ(A) = 2 and ρ ([ A | B]) = 2. So, ρ(A) = ρ ([ A | B]) = 2 < Number of unknowns. Hence the given system is consistent and has infinite number of solutions. Applications of Matrices: Consistency of System of Linear Equations by Rank Method
Theorem 1.14 (Rouché - Capelli Theorem)
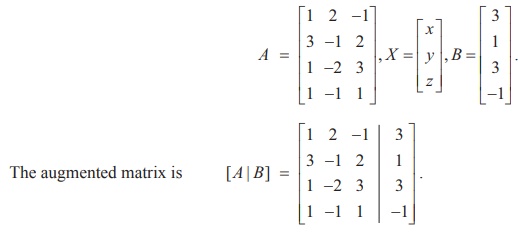
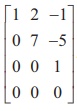. There are three non-zero rows in it. So ρ(A) = 3.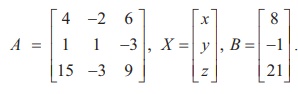 
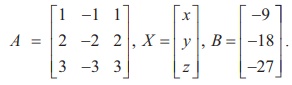
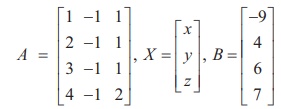
Example 1.33
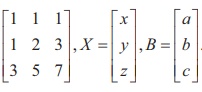
Example 1.34
Solution
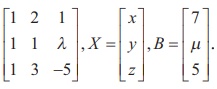
Tags : Definition, Theorem, Formulas, Solved Example Problems | Applications of Matrices: Consistency of System of Linear Equations by Rank Method , 12th Mathematics : Applications of Matrices and Determinants
Study Material, Lecturing Notes, Assignment, Reference, Wiki description explanation, brief detail
12th Mathematics : Applications of Matrices and Determinants : Matrix: Non-homogeneous Linear Equations | Definition, Theorem, Formulas, Solved Example Problems | Applications of Matrices: Consistency of System of Linear Equations by Rank Method
Solution of System of Linear Homogeneous and Nonhomogeneous Equations
Source: https://www.brainkart.com/article/Matrix--Non-homogeneous-Linear-Equations_39080/